
Pythagoras (6th century BC) observed that when the blacksmith struck his anvil, different notes were produced according to the weight of the hammer.
Number (in this case amount of weight) seemed to govern musical tone...
See if you can hear the sound in your imagination before it comes, by judging from the proportions of the string lengths. The first one's easy.

Again, number (in this case amount of space) seemed to govern musical tone. Or does musical tone govern number?
He also discovered that if the length of the two strings are in relation to each other 2:3, the difference in pitch is called a fifth:
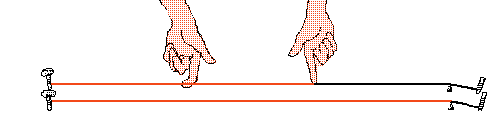
...and if the length of the strings are in relation to each other 3:4, then the difference is called a fourth.

Thus the musical notation of the Greeks, which we have inherited can be expressed mathematically as 1:2:3:4
All this above can be summarised in the following.

(Another consonance which the Greeks recognised was the octave plus a fifth, where 9:18 = 1:2, an octave, and 18:27 = 2:3, a fifth;)

This triangular figure of numbers in the shape of the Greek letter Lamda is the Tetrad of the Pythagorians.
As was discussed by Plato in his dissertation on the Composition of the Soul, it is a set of numbers whose relationships with each other seemed to summarize all the inter-dependent harmonies within the universe of space and time.
Thus to have established the relationship between music and space/number fired the imagination of the Pythagorians and was taken up especially by the School of Plato and the subsequent Neo-Platonists. Pythagoras himself wrote nothing which has survived, and so it is the Platonists we have to thank for recording and developing what had hitherto been passed down through two hundred and fifty years of oral tradition.
Pythagoras taught that each of the seven planets produced by its orbit a particular note according to its distance from the still centre which was the Earth. The distance in each case was like the subdivisions of the string refered to above. This is what was called Musica Mundana, which is usually translated as Music of the Spheres. The sound produced is so exquisite and rarified that our ordinary ears are unable to hear it. It is the Cosmic Music which, according to Philo of Alexandria, Moses had heard when he recieved the Tablets on Mount Sinai, and which St Augustine believed men hear on the point of death, revealing to them the highest reality of the Cosmos. (Carlo Bertelli, Piero della Francesca, p. 60.) This music is present everywhere and governs all temporal cycles, such as the seasons, biological cycles, and all the rhythms of nature. Together with its underlying mathematical laws of proportion it is the sound of the harmony of the created being of the universe, the harmony of what Plato called the "one visible living being, containing within itself all living beings of the same natural order".
For the Pythagorians different musical modes have different effects on the person who hears them; Pythagoras once cured a youth of his drunkenness by prescribing a melody in the Hypophrygian mode in spondaic rhythm. Apparently the Phrygian mode would have had the opposite effect and would have overexcited him. At the healing centers of Asclepieion at Pergamum and Epidauros in Greece, patients underwent therapy accompanied by music. The Roman statesman, philosopher and mathematician, Boethius (480-524 A.D.) explained that the soul and the body are subject to the same laws of proportion that govern music and the cosmos itself. We are happiest when we conform to these laws because "we love similarity, but hate and resent dissimilarity". (De Institutione Musica, 1,1. from Umberto Eco, Art and Beauty in the Middle Ages. p. 31).
